Demystifying this often misunderstood theorem.

Who doesn’t love free lunch? You don’t have to cook or spend any of your hard-earned money. It’s a great deal for anyone! The truth is unless if you count special talks and lectures in graduate school that promise free pizza, there is no free lunch in machine learning.
The “no free lunch” (NFL) theorem for supervised machine learning is a theorem that essentially implies that no single machine learning algorithm is universally the best-performing algorithm for all problems. This is a concept that I explored in my previous article about the limitations of XGBoost, an algorithm that has gained immense popularity over the last five years due to its performance in academic studies and machine learning competitions.
https://towardsdatascience.com/why-xgboost-cant-solve-all-your-problems-b5003a62d12a
The goal of this article is to take this often misunderstood theorem and explain it so that you can appreciate the theory behind this theorem and understand the practical implications that it has on your work as a machine learning practitioner or data scientist.
The Problem of Induction
Strangely enough, the idea that may have inspired the NFL theorem was first proposed by a philosopher from the 1700s. Yes, you read that right! Not a mathematician or a statistician, but a philosopher.
In the mid-1700s, a Scottish philosopher named David Hume proposed what he called the problem of induction. This problem is a philosophical question that asks whether inductive reasoning really leads us to true knowledge.
Inductive reasoning is a form of reasoning where we draw conclusions about the world based on past observations. Strangely enough, this is exactly what machine learning algorithms do. If a neural network sees 100 images of white swans, it will likely conclude that all swans are white. But what happens if the neural network sees a black swan? Now the pattern learned by the algorithm is suddenly disproved by just one counter-example. This idea is often referred to as the black swan paradox.

Hume used this logic to highlight a limitation of inductive reasoning — the fact that we cannot apply a conclusion about a particular set of observations to a more general set of observations.
“There can be no demonstrative arguments to prove, that those instances, of which we have had no experience, resemble those, of which we have had experience.” — David Hume in A Treatise of Human Nature
This same idea became the inspiration for the NFL theorem for machine learning over 200 years later.
Application to Machine Learning by Wolpert
In his 1996 paper, The Lack of A Priori Distinctions Between Learning Algorithms, Wolpert introduced the NFL theorem for supervised machine learning and actually used David Hume’s quote at the beginning of his paper. The theorem states that given a noise-free dataset, for any two machine learning algorithms A and B, the average performance of A and B will be the same across all possible problem instances drawn from a uniform probability distribution.
Why is this true? It goes back to the concept of inductive reasoning. Every machine learning algorithm makes prior assumptions about the relationship between the features and target variables for a machine learning problem. These assumptions are often called a priori assumptions. The performance of a machine learning algorithm on any given problem depends on how well the algorithm’s assumptions align with the problem’s reality. An algorithm may perform very well for one problem, but that gives us no reason to believe it will do just as well on a different problem where the same assumptions may not work. This concept is basically the black swan paradox in the context of machine learning.
The limiting assumptions that you make when choosing any algorithm are like the price that you pay for lunch. These assumptions will make your algorithm naturally better at some problems while simultaneously making it naturally worse at other problems.
The Bias-Variance Tradeoff
One of the key ideas in statistics and machine learning that is closely related to the NFL theorem is the concept of the bias-variance tradeoff. This concept explores the relationship between two sources of error for any model:
- The bias of a model is the error that comes from the potentially wrong prior assumptions in the model. These assumptions cause the model to miss important information about the relationship between the features and targets for a machine learning problem.
- The variance of a model is the error that comes from the model’s sensitivity to small variations in the training data.
Models with high bias are often too simple and lead to underfitting, while models with high variance are often too complex and lead to overfitting.

As demonstrated in the image above, a model with high bias fails to properly fit the training data, while a model with high variance fits the training data so well that it memorizes it and fails to correctly apply what it has learned to new real-world data. The optimal model for a given problem is one that fits somewhere in between these two extremes. It has enough bias to avoid simply memorizing the training data and enough variance to actually fit the patterns in the training data. This optimal model is the one that achieves the lowest prediction error on the testing data for a given problem by optimizing the bias-variance tradeoff as shown below.
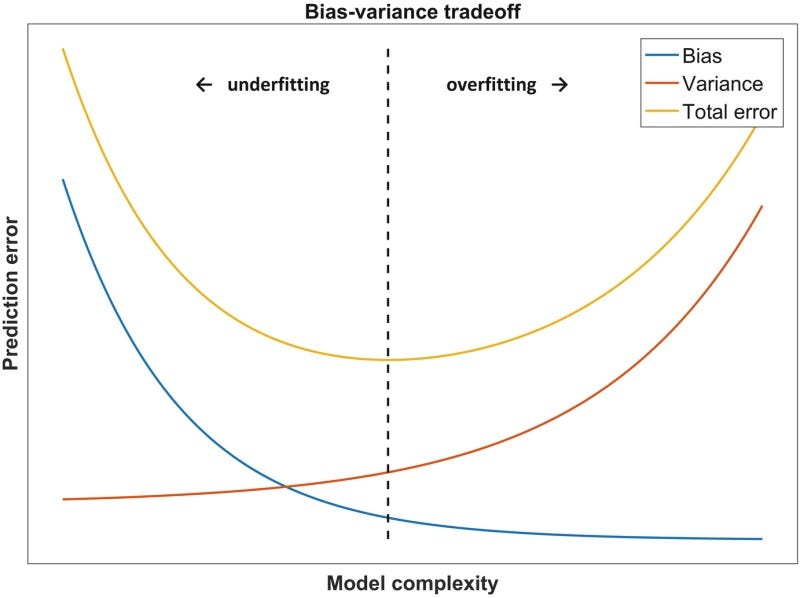
Obviously, every machine learning problem has a different point at which the bias-variance tradeoff is optimized and the prediction error is minimized. For this reason, there is no super-algorithm that can solve every machine learning problem better than every other algorithm. Every algorithm makes assumptions that create different types and levels of bias, thus making them better suited for certain problems.
What “No Free Lunch” Means for You
All of this theory is great, but what does “no free lunch” mean for you as a data scientist, a machine learning engineer, or someone who just wants to get started with machine learning?
Does it mean that all algorithms are equal? No, of course not. In practice, all algorithms are not created equal. This is because the entire set of machine learning problems is a theoretical concept in the NFL theorem and it is much larger than the set of practical machine learning problems that we will actually attempt to solve. Some algorithms may generally perform better than others on certain types of problems, but every algorithm has disadvantages and advantages due to the prior assumptions that come with that algorithm.
An algorithm like XGBoost may win hundreds of Kaggle competitions yet fail miserably at forecasting tasks because of the limiting assumptions involved in tree-based models. Neural networks may perform really well when it comes to complex tasks like image classification and speech detection, yet suffer from overfitting due to their complexity if not trained properly.
In practice, this is what “no free lunch” means for you:
- No single algorithm will solve all your machine learning problems better than every other algorithm.
- Make sure you completely understand a machine learning problem and the data involved before selecting an algorithm to use.
- All models are only as good as the assumptions that they were created with and the data that was used to train them.
- Simpler models like logistic regression have more bias and tend to underfit, while more complex models like neural networks have more variance and tend to overfit.
- The best models for a given problem are somewhere in the middle of the two bias-variance extremes.
- To find a good model for a problem, you may have to try different models and compare them using a robust cross-validation strategy.
Sources
- The Stanford Encyclopedia of Philosophy, The Problem of Induction, (2018).
- DeepAI, Black Swan Paradox Definition, (2020), deepai.org.
- D. Hume, A Treatise of Human Nature, (1739), Project Gutenberg.
- D. H.Wolpert, The Lack of A Priori Distinctions Between Learning Algorithm, (1996), CiteSeerX.